IIR Filter Design pt 1.1 – Region of Convergence and BIBO stability

I want to make a quick aside to talk about region of convergence and bounded-input bounded-output (BIBO) stability. When we’re discussing IIR filters, or you know, any difference equation things. it’s worth talking about whether or not over time, is this filter going to be stable? If we feed it whatever signal, so we expect it to behave nicely, or will it just grow and explode into infinity even if we feed it the tiniest thing?

I don’t plan on talking about issues caused by quantization error, though that is somewhat important, that’s a whole different ballgame. We can talk about that later.

Let’s bring up a trivial low pass filter,

You can intuitively reason that this is probably a stable filter given a bounded (say, finite length, if that’s easier to imagine) input. If you pass it a Kronecker delta (reminder: , all other time indices it’s 0), your results will end up something like



And so on. You see it ever decreasing, so yeah, chances are that’ll never blow up to infinity, it’ll just get closer to zero.
Using the standard z-transform and doing a little rearranging, we can get

Using a pole-zero graph, we plot points (in this case, a single point since we have a trivial example) where z would cause H(z) to be zero or infinity. We have a single pole here, , and we plot that on our chart.

We can see the pole sitting JUST inside of the unit circle.

Now let’s do the polar opposite. Maybe something really terrible.

You can imagine this blowing up very quickly weirdly with a Kronecker delta.



That’s not going to be pretty, alternating between infinity and negative infinity. And all we passed it was a delta! We the same z-transform and rearrange as before, we can get

We can see easily that there’s a pole , so… that’ll be weird.

We can see that the pole is sitting somewhere way outside the unit circle in this case for this unstable dumb filter.

I’m going to state some rules of thumb IIR filters given a signal that can actually exist (i.e. a CAUSAL system)

1. The region of convergence for a causal filter is all of the area on that pole zero graph outside of a circle with radius of distance from origin to furthest pole. Essentially, think the smallest circle that can contain all of the poles on the pole zero chart, and all of the area outside of that NOT including the circle is the region of convergence (for signals that only exist… uh, like “ahead” of time, like n time index less than 0, region of convergence is going inwards towards origin from inner-most pole rather than outwards to infinity. For two-sided signals, the ROC is circle from inner most pole to outermost pole)
2. Since the pole zero plot is representative of the values z can be of the z-transform, the unit circle represents z such that , which incidentally is the discrete-time Fourier transform of the filter.
3. if the region of convergence INCLUDES the unit circle, meaning all poles of the filter are within the unit circle, the IIR filter is considered BIBO stable AND the discrete-time Fourier transform of the filter exists (though if you leave it in the form with just a bunch of exponential functions and coefficients your professor is going to get mad).

So why is this useful? Say you have a complicated filter, lots of numerator and denominator coefficients for . If you factor apart the top and bottom parts of and get a bunch of poles and zeros, you can immediately tell if something is stable or not, on top of also having a pretty good guess at what the filter does by just looking at location of poles and zeros (guessing at filter type will come later…).

Interestingly enough, I haven’t mentioned zeros yet. Zeros are ok for stability. Think about it, your zero will just guarantee at a point, we’re equal to zero, rather than if our z value hits a pole, our filter magnitude may shoot to infinity. With an FIR filter, if you do the z-transform, you can see that you’re only going to have zeros, no poles. With an FIR filter, you also know that whatever your input is, your output will die off after some number of taps if the input dies off; thus FIR filters are always BIBO stable, and correspondingly don’t have any poles inside or outside of the unit circle to worry about.

IIR filter design pt 1 – analog filter prototypes

Let’s just jump into design, I’ll talk about digital filter implementation things later on.

So the design of a digital filter generally hinges on starting with an analog filter, and transforming the result into a digital filter by a mapping of the Laplace transform variable, generally s, to Z-transform variable z. There are three base filters that ppl typically use. For simplicity, I’m going to assume the Fourier transform. Also, filter order is n.

Butterworth filters have a nice smooth surface, no ripples, and impulse response are based off of Bessel functions, which explains the smoothness (you can see this best with a 1st order Butterworth filter, as the impulse response is actually a zero-order modified Bessel function of the second kind). They are the simplest to work with, but because of the lack of rippling, getting a desired response at the transition point may require a higher filter order, i.e. more coefficients, which results in more computation. Butterworth low pass filters have the following equation to describe the gain, where is the cutoff frequency:

Chebychev filters are either equiripple in the passband or stopband, and then flat like Butterworth on the other. Type 1 has ripple in the passband and flat elsewhere, type 2 is flipped. This filter depends on Chebychev polynomials, which have a closed form of the following

but that bit of added complexity makes Butterworth better for simple tutorials. Sorry I couldn’t figure out how to make piecewise function notation work in WordPress.

Type 1 can be described using the following gain, where is the ripple factor, i.e. how much ripple would you allow, and is the Chebychev polynomial:

Type 2 can be described using the following gain:

Basically you can see the ripple part of Chebychev filters is governed by the cosine part of the Chebychev polynomial, and the flat part is governed by hyperbolic cosine.

Elliptical filters are equiripple throughout and have the best tradeoff for ripple and transition width, assuming you are willing to put up with ripple in the first place. They have the following gain:

where is the Jacobi elliptic function of n-order. I have no idea how to describe these in a concise way, but they are widely implemented in filter design suites and are tabulated in tons of places, so you don’t have to know the nitty gritty details to implement elliptical filters.

So i described the three analog filter prototypes people generally use for IIR filter design. I’ll try to put up some pictures to show the differences before the next post, but next time I’ll discuss the transformations used to go from analog to digital filter. The post after that will probably be working through an example using lowpass Butterworth filter.

I apologize for being lazy with the programming and graphing and whatever but my life got busy, so I’ll try to update and stuff but the posts might be a little bare, sorry.

Infinite Impulse Response (IIR) digital filters

Break from statistics. I want to talk about digital signal processing again. So I talked about FIR filters before, let’s talk about IIR filters. Like how to recognize them, analysis, maybe things like direct form type I and II later, and then at least simpler design like Butterworth IIR filter design, and a mention of the transforms to go from analog to digital domain.

So what is an infinite impulse response filter? Well, it’s a filter such that a resulting signal from passing something through doesn’t really ever die off completely. Lemme bring back the easy example I used in my FIR filter post.

Let’s say our input is a Kronecker delta such that and everywhere else it’s just nothing. When , . At the next time step, . And the next time step, . And so you can see with every time step, our resulting signal is getting smaller, and it does converge to 0, but it just keeps going and going.

So how can we find the impulse response? We can use the z-transform like we did for FIR filters.

We know our impulse response is output over input, so

And of course, if the region of convergence for our z-transform includes the unit circle, we can find the discrete-time Fourier transform simply by replacing z with ,

And just like that, we have our impulse response for our IIR filter. Yeah, this one is kind of trivial but it’s just for teaching purposes.

So how do we know if our IIR filter is stable? With FIR filters, we knew it was going to be stable no matter what. The output signal would end, assuming input was bounded and finite already. If we look at our IIR filter Z-transform, given a more complex one, we can see that with a polynomial on top and bottom, we will have zeros such that some complex values of z will make the filter equal to 0, and we will have some poles such that some values of z make the filter shoot to infinity. The general rule is that given a CAUSAL filter, like one that doesn’t somehow go backward in time, if the poles are inside of the unit circle, the unit circle is included in the region of convergence and our filter is stable. So that’s cool. I mean, if zeros are inside of the unit circle, then we also have less of a phase mess-up problem too, but that’s less of a problem than unstable filters.

So what are the pros and cons of IIR filters? In a lot of situations, IIR filters can get the desired filter response wanted using significantly fewer filter coefficients than FIR filters. In many situations, IIR filters that have been turned into biquads or filter banks, basically split into packs of smaller IIR filters, are pretty computationally efficient if you don’t have the luxury of doing zero-padded FFTs for FIR filters.

The downsides? IIR filters tend to be pretty sensitive to limitations of computer numbers. If the machine precision isn’t good enough, the actual filter behavior may not function as planned. Even if the filter acts like you’d expect at the beginning, the numerical precision thing leads into a feedback problem, say the filter behavior EVENTUALLY turns into garbage because of numerical limitations. This can be solved with a zeroing of values, basically resetting the filter, at some point, but that may mean tossing out information. Additionally, IIR filters aren’t conveniently linear phase or zero-phase like FIR counterparts can be designed, so if you need real-time signal processing, get ready to have some phase changes. These can be minimized if the filter is designed such that zeros are within the unit circle. Additionally, if the real-time requirement isn’t there, you can do a forward-backward filter process to have a zero-phase filter by simply doing the filter, and then using a time-reversed version of the filter.

I’m too lazy to fire up python or matlab, but you can use the examples from the FIR filter to do analysis of IIR filters. freqz(b,a,n) in both python and matlab are designed such that b is a vector of coefficients in the numerator of H(z), a is a vector of coefficients in the denominator of H(z), and n is some number of samples that basically lets you set a resolution to look at. Note that for FIR filters, we set a = 1 because we don’t have any denominator to H(z) to worry about.

Generating random samples pt. 3 – Metropolis-Hastings algorithm

So last time I talked about rejection sampling for generating random samples of a specific distribution, starting from another distribution. We talked about what made it suck, and really, if you are going to do rejection sampling, you might as well head straight to Metropolis-Hastings, it’s basically an improved version with no downsides when compared to rejection sampling.

So the Metropolis-Hastings algorithm is another Monte Carlo method of generating samples, and really, it’s basically rejection sampling with a minor change. So I’ll go over the gist of it, and then point out the change, and why Metropolis-Hastings even works.
The algorithm is as follows.
Given a target PDF of and SYMMETRIC densities of (symmetric meaning ) that we are drawing samples from, where g is conditioned on the previous sample we had accepted,
1. Get a sample x from , and a sample from a uniform random variable between 0 and 1, i.e. , which we’ll MIGHT be using to make our decision whether or not to keep or reject the new sample.
2. Check if we keep the sample; if , such that the PDF of the new sample is larger than the previous one, we keep our new sample straight up. Otherwise, we need to do a check against our uniformly distributed value; if our uniformly distributed random sample , then we keep the new sample x. Otherwise, we reject x.
3. If we kept the previous sample, is replaced with the x we just got. Go back to step 1 and keep doing it until we have enough values.

A common example of is a Gaussian distribution with a mean of . Then the resulting process will be something of a random walk, which very nicely lines up with the Markov chain proof of correctness for this algorithm. I’M not going to prove it is right, but there certainly is proof, this process is pretty old.

So what’s the big deal? We changed our criterion for keeping samples. On inspection, you’ll note that we don’t need a dumb scaling constant anymore, and assuming we chose nice source and target distributions to work with, our acceptance rates will be much nicer than before.

But you might think, hey, if we accept more stuff like this, how can we guarantee Metropolis-Hastings even gives us samples pertaining to our target distribution?

In truth, the Metropolis-Hastings algorithm is loosely construction a Markov chain system like the ones we’ve suggested before. What we are doing is moving from state-to-state as we accept samples, and our Markov chain is constructed in such a way such that the stationary distribution of the Markov chain will be the target distribution! Of course, for a target PDF, since it’s a continuous function, this is not intuitive to see, but working with a discrete PMF, say, something trivial like simulating a fair 6-sided die by choosing a conditional such that each roll is biased (evenly, like the PMF is simply being shifted over a single value at a time from 1 to 6) more towards the number last rolled, it’s very possible to construct the transition matrix and see that the end stationary distribution of the system will be that of a fair die. An example would be a transition matrix like this…

Even though the die is a biased turd, if we generated dice rolls over time with this transition matrix, the stationary distribution in the end would be a nice uniform fair die.

So what are the downsides to this? Well, samples tend to be correlated with their neighboring samples, so if you want uncorrelated samples, you sort of have to give the samples a good shuffle. Additionally, the first bunch of samples generated clearly won’t be distributed as we’d want because the Markov chain hasn’t had time to hit a stationary distribution, so expect to have a burn-in period of running the algorithm, throwing things away, and then getting samples to use.

Hell, I’m lazy, you can fix my previous function to work with Metropolis-Hastings if you really want, the change is trivial and my previous function wasn’t great anyways. I wrote it in maybe a couple minutes.

Next time, if I get the chance, I will discuss Gibbs sampling and wrap up what I want to say on generating samples of a target distribution.

Generating random samples pt. 2 – rejection sampling

So I covered basic inverse transform method of generating samples of a specific distribution, and all that required was basically knowing the CDF and inverting the function, followed by feeding it uniformly distribution samples from 0 to 1 and that was that. However, some distributions are difficult or nearly impossible to invert analytically, so… where does that leave us?

So rejection sampling, also known as the acceptance-rejection method, is a Monte-Carlo method that allows us to simulate generation of samples of basically any probability density. The idea behind it is that we can sample a random variable by sampling uniformly underneath the graph of a density function.

The gist of the algorithm is as follows:
Given a target PDF of , a normalization constant M that effectively adjusts frequency of rejection when increased, and a density of that we are drawing samples from,
1. Get a sample x from , and a sample from a uniform random variable between 0 and 1, i.e. , which we’ll be using to make our decision whether or not to keep or reject the new sample.
2. Check if we keep the sample; if our uniformly distributed random sample , then we keep x. Otherwise, we reject x.
3. Go back to step 1 and keep doing it until we have enough values.

You can see from the algorithm that increasing M would decrease the probability of retaining generated samples, but M additionally has to be set such that so that step 2 actually makes sense, avoiding violating axioms of probability.

An example written in Python is available below. Basically, it wants a function f_x passed in representing a 1D PDF of the target distribution we want. We are using Gaussian random variables for our drawn g_x function because the domain is infinite and we can fine-tune where we sort of want our concentration using the parameters. Then M and number of samples is up to the user, though if M proves to be too small, M is doubled and the function is called recursively in hopes that things will work out better next time.

import numpy as np

def rejection_sampling_1D( f_x, g_var, g_mean, M, num_samples ):
    ''' does rejection sampling using a Gaussian distribution as  the
    underlying density, given a target density function f_x and a number of
    samples we want generated.'''
    g_x = lambda x: 1/np.sqrt(2*np.pi*g_var)*np.exp(-(x-g_mean)**2/(2*g_var))
    good_samples = 0;
    # do shit until we have enough samples
    keepers = np.zeros(num_samples)
    while good_samples < num_samples:
        # generate a new sample using our underlying distribution
        new_samp = np.random.randn(1)*np.sqrt(g_var)+g_mean
        # generate a new uniform
        new_check = np.random.rand(1)
        # first, let's make sure M is big enough
        while f_x(new_samp)/g_x(new_samp)/M > 1:
            M = 2*M
            return rejection_sampling_1D( f_x, g_var, M, num_samples )
        # now let's check if our stuff actually works.
        if new_check >= f_x(new_samp)/g_x(new_samp)/M:
            keepers[good_samples] = new_samp
            good_samples = good_samples + 1
        else:
            continue
    return good_samples

So what’s wrong with this? The first major problem is that if distributions are chosen poorly, like if isn’t remotely related to , a lot of samples may be generated and tossed away, wasting computation cycles, or a lot of samples may be taken in a specific area, getting us a lot of unwanted samples. The former result is magnified immensely once we begin talking about multidimensional random vectors, running straight into the curse of dimensionality, where chances are corners and edges of our multidimensional density simply don’t get the coverage we were hoping for.

Next time, we will talk about Metropolis-Hastings method for generating random samples. It’s better than rejection sampling, and it also partially ties into our Markov Chain talks before, though I won’t get into that in too much detail. If I get a chance, I may also talk about Gibbs Sampling in a post afterwards.

Generating random samples pt. 1 – Inverse Transform Method

Heck, I feel like talking about something simple today. Let’s do something relatively easy I don’t have to generate code for because it’s late and now I have a job.

So let’s say we have a continuous random variable X with a probability density function and a cumulative density function . We can suggest that random variable Y is a function of X such that , meaning the probability of the random variable X being less than or equal to X is equal to Y. Thanks to axioms of probability, we can see that Y is not only distributed only between 0 and 1, but Y has a uniform probability distribution (you can work out the function of a random variable using CDF method and you’ll get things that cancel out and suggest that you have a uniform distribution, regardless of what X is distributed. Something like

though I don’t know how legit that is).

So the inverse transform method basically says so if we generate a uniform random variable U, we can generate a random variable X with a PDF of and CDF of as described above but finding . So we find the inverse of the CDF of X, and just feed it uniform random variables between 0 and 1.

The easiest example I can think of is as follows: say we want to generate exponential random variables. We know the PDF is , and the CDF is . We find the inverse of the CDF, so . If we plug in uniformly generated numbers, which are generally readily accessible on a computer by some means of pseudorandom number generator, we get exponentially distributed random variables.

There are two glaring problems with this: firstly, this is for continuous random variables, so it’s sort of limited in scope, even though discrete random variable generation usually isn’t difficult to simulate in the first place with just a little critical thinking. Secondly, we need to solve for the inverse of the CDF for every distribution we want to generate samples for. What if the CDF is something ridiculous to deal with, like Gamma distribution or Nakagami-m distribution? We need some other ways to generate samples.

Next time, I’ll probably cover rejection sampling, then Metropolis-Hastings algorithm the post after that.

On stationary distributions of discrete Markov Chains

I feel like I need to publish something quick, so I’ll just discuss stationary distributions for Markov Chains real quick before my orientation stuff at Cisco in California. I don’t necessarily know if I have time to make a post while I’m there.

We’ve discussed Markov Chains previously. Given a set of states, say n states such that where S is the set of all states we care about, we have a transition matrix that is n x n elements, say a matrix A like the following:

where the transition matrix entry is the probability of being AT state i, and moving to state j. REMEMBER THIS, because some books like to refer to it the other way around, like i is the target state and j is the previous state, and that changes our notation up entirely here.

For simplicity, you can assume our Markov Chain is time-invariant, meaning the probabilities in the transition matrix don’t change over time. I believe what we are discussing here will hold, but definitely not in a obvious and conveniently calculable way, like there’s going to be symbols and stuff, and potentially you’d probably have to prove that the markov chain remains positive recurrent over time, weird shit, let’s not get into that. Let’s assume we have a nice matrix full of constants that don’t change with each time step.

So say we have a starting distribution of what state we might be in, a row vector x such that . The subscript of X indicates which time step we’re talking about, and 0 is obvious the start. We can find the probability of being in whatever state at time step t by doing the following
so we have a row vector multiplied by our A transition matrix to get us another row vector with the changed probabilities of being at each state at whatever time step. So that’s cool, right? Very handy in terms of calculation. Assuming your transition matrix is legit, like the rows add up to 1 properly, then your X elements should also sum up to 1 all the time. You can prove this but it takes some work, just accept it for now.

So a stationary distribution is when we have some row vector Y such that , so when you multiply the row vector Y with the transition matrix, there is no change to the elements of Y, the probabilities remain the same. This stationary distribution typically comes up as a limiting distribution where . So yeah, if you want to brute force your way to a stationary distribution, you can calculate it on a computer by doing matrix multiplies over and over until hitting some convergence point.

But linear algebra people should recognize that Y here is actually a LEFT eigenvector! You can solve for this simply by solving for the (right) eigenvectors of , the transpose of the transition matrix, and finding the eigenvector associated with eigenvalue 1, and normalizing it such that it is a legit discrete probability vector. So there’s a clear relation of linear algebra to Markov chains.

Obviously, there has to be a catch to this bit, right? So there are three things that could happen with stationary Markov chains.
1. unique stationary distribution
2. multiple unique final distributions
3. oscillating/alternative final distributions

The uniqueness of the stationary distribution is only guaranteed iff the MC is positive-recurrent. What does that even mean? The simplest way to find it is by making sure each state is reachable at any time, i.e. they are all recurring states, and that the periodicity of each state going back to itself eventually has a greatest common factor of 1 (like there could be a state that goes back to itself potentially even 2 steps at the quickest, but somebody else could only do it in minimum 3 steps, then the GCF is 1). In linear algebra terms, this effectively guarantees the matrix is full rank, geometric multiplicity of eigenvalue 1 is 1 (there’s only 1 eigenvector associated with eigenvalue 1), and there’s no weird thing involving eigenvector -1.

How do 2 and 3 even occur then? 2, if you effectively have transient states, or just completely separable Markov chains you happened to put into the same matrix (like with 5 states, if states 1-3 communicated amongst themselves and 4,5 communicated only between themselves), you will end up with more than 1 stationary distribution at the end. In case 3, if there’s some periodicity going on, then clearly it’s possible that the Markov chain will have some alternating with each time step and not actually be stationary by the end, though it will have converged to a set of probability vectors. Generally, you may end up with a eigenvector for eigenvalue 1, and then an eigenvector for eigenvalue -1 that will represent the change in the distribution with every time step.

Interesting Applications of Amplitude Modulation of Signals

I had a hard time thinking about what to write, and I settling with amplitude modulation. So let’s get down to it.

Simply put, amplitude modulation of a signal causes a signal to have sinusoidal fluctuations in amplitude. The simplest form of AM can be shown in this equation, given a signal

is some radian frequency oscillation rate, is a possible phase offset, and is obviously time.

I made a plot below that visibly shows the effects of basic amplitude modulation below on a simple triangle wave. Code is available at the bottom of the page. You can see the ENVELOPE of the signal, i.e. the original triangle wave, though it goes positive and negative thanks to the cosine wave. Additionally, in the frequency domain, you can see the fat spike of the triangle wave getting spun up to the frequency of the cosine wave! This is how basic AM radio works, the original signal is spun up to a higher carrier frequency before being transmitted over the air!

Amplitude modulation isn’t described only by the equation above, it’s a blanket term for affecting the amplitude of a signal with a sinusoidal function, so as you can imagine, different applications get different equations for different purposes.

The equation given above has a use in audio effects known as “TREMOLO.” You can buy a tremolo pedal for electric guitars, and a lot of nicer solid-state or DSP-based amplifier systems like Line6’s Spider series generally have a tremolo function built in. The most obvious use of it is in the beginning of Boulevard of Broken Dreams by Green Day, from the 2004 album American Idiot. Aside from arguments concerning musical taste, the simple chord progression makes it very clear what tremolo effects sound like.

In radio, amplitude modulation takes a huge turn into complexity land because of its various applications and uses in both analog and digital radio. The simple equation above is known as double-sideband suppressed carrier, as opposed to double-sideband AM which is like

There are other types of analog AM like single-sideband varieties. Say, single-sideband suppressed carrier with an equation like this:

The varying radio types require different receivers and have different power requirements, not to mention analog implementation of transmitters is also sort of rigid in terms of design. Modern digital communications using pulse amplitude modulation or quadrature amplitude modulation also build on the AM idea, but using a fixed constellation size and flexible parameters, they allow for much more reliable communications than analog methods in general, not to mention basic nice things you get from putting data into bits (forward error correction, etc).

I’m sure there are other useful things that amplitude modulation can do, but those are the two I’m most attuned with.

Oh yeah, the code I promised for making those plots.

# -*- coding: utf-8 -*-
"""
Created on Tue Mar 18 23:46:58 2014

@author: joshua
"""

import numpy as np
import matplotlib.pyplot as plt
# initialize a triangle wave
triangle = np.hstack( (np.zeros(15), np.linspace(0,1,50), np.linspace(1,0,50), np.zeros(15)) )
n = np.size(triangle)
# initialize a cosine wave
the_cos = np.cos(2*np.pi*.2*np.arange(n))
# multiply 
the_result = triangle*the_cos
# plot triangle
plt.figure()
plt.subplot(3,1,1)
plt.plot(np.arange(n), triangle)
plt.xlabel('sample index')
plt.ylabel('amplitude')
plt.title( 'triangle wave' )
# plot cosine
plt.subplot(3,1,2)
plt.plot(np.arange(n), the_cos)
plt.xlabel('sample index')
plt.ylabel('amplitude')
plt.title( 'carrier cosine' )
# plot both together
plt.subplot(3,1,3)
plt.plot(np.arange(n), the_result)
plt.xlabel('sample index')
plt.ylabel('amplitude')
plt.title( 'AM result' )
plt.tight_layout()
# save it
plt.savefig('am_demo_1.png')
# plot triangle FFT
plt.clf()
plt.subplot(3,1,1)
plt.plot(np.linspace(0, 2*np.pi, num=n, endpoint=False), np.abs(np.fft.fft(triangle)))
plt.xlabel('freq in radians')
plt.ylabel('magnitude')
plt.title( 'triangle wave in frequency' )
# plot cosine FFT
plt.subplot(3,1,2)
plt.plot(np.linspace(0, 2*np.pi, num=n, endpoint=False), np.abs(np.fft.fft(the_cos)))
plt.xlabel('freq in radians')
plt.ylabel('magnitude')
plt.title( 'cos in frequency' )
# plot both FFT
plt.subplot(3,1,3)
plt.plot(np.linspace(0, 2*np.pi, num=n, endpoint=False), np.abs(np.fft.fft(the_result)))
plt.xlabel('freq in radians')
plt.ylabel('magnitude')
plt.title( 'AM result in frequency' )
plt.tight_layout()
# save it
plt.savefig('am_demo_2.png')

(Good) FIR Filter Design pt 3: Parks-McClellan algorithm

I’ve covered windowing FIR design, frequency sampling FIR design, and a research paper that was awful. So let’s get to the good stuff.
Parks-McClellan uses the Remez exchange method for designing an optimal FIR filter. There’s a lot to it, so let’s try to cover some background in a loose sense quickly. I’ll present stuff, but with no proof, since this shit is actually complicated and covered widely elsewhere.

The alternation theorem says for a polynomial in sum form where r is the order of the polynomial and a values are coefficients of the polynomial and an error function defined as where D is the desired “optimal” function of x, and W is how we are weighting the error, is a unique polynomial of r order that minimizes iff exhibits AT LEAST alternations.

Intuitively, for our purposes, that means we can design a filter that minimizes its error in comparison with an ideal filter with L coefficients that has AT LEAST L+2 alternations (basically, we need the error to hit our ripple value L+2 times or more). If we don’t have at least L+2 alternations, then the filter we designed does not minimize the error and we know we can do better than that. Interestingly enough, since we know L degree polynomial can only have L-1 zero-slope critical points at most, counting band edges in our filter design constraints as possible extremal points, we can have a max of L+3 alternations in our designed filter.

With that in mind, we want to model our linear-phase filter design problem as a polynomial interpolation problem. Let’s design the filter such that it is zero-phase, i.e. the frequency response is all real. That implies that the Fourier transform is something like this:

. Then, if we have , then obviously we can see we have a polynomial on our hands. We can define a linear polynomial interpolation problem at extremal points in frequency (for simplicity, let’s set it up Ax=b just like a Vandermonde interp problem) such that

And then you could find the polynomial coefficients (i.e. the new filter) and check if its good. If not, well, see where the new extremal frequencies are, and try again. It’ll converge.

So the entire Parks-McClellan algorithm can be broken down as the following:

0. Set filter constraints. Say, you want a lowpass filter, we want between and between .
1. Choose a odd positive integer L for filter length (odd so we can do this zero-phase filter design without weird problems occurring).

2. Choose some starting extremal points, basically points in the frequency response of the filter that will hit our high ripple or low ripple. Normally this is just chosen to be evenly spaced initially since we need to do several iterations to converge anyways.

3. Perform polynomial interpolation to find new filter coefficients according to our constraints and our filter ripple value. While Vandermonde interpolation seems to be the obvious choice here, Parks-McClellan actually used Lagrange interpolation to do this efficiently back in the day.

4. Find the error function, i.e. subtract frequency response of newly designed filter from the constraints we desired at the beginning, and find all of the points in this error function that are where is our ripple value. These points are now your new extremal points.

5. If the extremal points found in step 4 don’t match what you had before, or this is the first loop through, go back to step 3, but now working with new extremal points to get a new set of filter coefficients and ripple. Otherwise, you found your ideal filter.

There are bits and pieces of this algorithm I haven’t explained like the derivation of the polynomial interpolation using Lagrange interpolation, but really, you guys shouldn’t be implementing your own Parks-McClellan anyways. There are version of it in every language at this point.

In MATLAB, newer versions would call “firpm()” while older ones still called “remez()”. Python SciPy users would call “remez()” from the signal submodule.

Here’s an example of MATLAB usage for a lowpass filter.

freq = [0 .4 .6 1];
constraint = [1 1 0 0];
L = 15;
h = firpm( L, freq, constraint );

Here’s an example of Python usage, same lowpass filter.

import numpy as np
import scipy.signal as sp
numtaps = 15
bands = np.array([0, .2, .3, .5])
desired = np.array([1, 1, 0, 0])
h = sp.remez( numtaps, bands, desired )

It’s really easy, and it gets you the best result, so just use these for FIR filter design. Don’t even bother with the other dumb methods. Note that remez in python uses a funny Hz notation for a lot of its things with 1Hz sampling rate default, and firpm does everything in terms of 2Hz sampling rate by default. It’s weird, but whatever, as long as you get things straight, it works.

(Bad) FIR Filter Design pt 2: Snake Oil Research papers…

Before I make a post on Parks-McClellan filter design, I want to talk about a paper I found awhile back when I was looking around on the internet for existence of a 2-dimensional or N-dimensional filter design equivalent to Parks-McClellan. I found a paper called Equiripple FIR Filter Design by FFT Algorithm (microsoft academic link , too lazy to find the paper), and it promises Parks-McClellan like filter results but using a much simpler method that simply relies on FFTs. This is the first time I read a not-already-proven research paper (say, the original OFDM paper or the “Gap” paper by Forney), and it was too good to be true. In fact, it actually sucks, and it’s easily apparent if you think about the process, but the paper make it sound so legit. I couldn’t even recreate the results with both my code and an implementation from their university that I found, so this is complete bullshit.

The algorithm can be summarized as follows:

0. Decide on a ripple 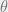, a large N number of frequency points, and an L<N length of an FIR filter you'd like, L being an odd number so we can have a linear phase or zero phase FIR filter.

1. initialize your ideal filter, using a large number of discrete frequency points, say N points. Of course, for a low pass filter, that simply means make a rect function around the 0 index.

2. IFFT your filter, and window it to the number of samples you want your zero-phase FIR filter to be. Say, if you want a filter of L samples such that L is odd, then we want samples N-floor(L/2):N-1 and 0:floor(L/2), basically around the 0 index still. Thanks to our IFFT, the filter should be symmetric and zero-phase. At this point, if you looped back here already, check for convergence against the previous windowed result. If converged, break, your filter is done.

3. FFT the filter, and in frequency, subtract the filter magnitude (it should all be real since we're doing zero-phase) from the ideal filter we had at the beginning and wherever the error is greater than 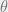ripple, force it to be , and wherever the error is less than 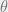ripple, force it to be .

4. Go back to step 2, and check for convergence.

This system basically does windowing filter design AND frequency sampling in an alternating fashion to come up with a filter. Combining 2 shitty filter design methods does NOT get you a result that is even remotely as good as Parks-McClellan. Just the windowing alone results in getting ridiculous Gibbs phenom, and let's not even forget we have no idea what effects are resulting from the frequency constrained design part. This method does converge, but the result is garbage.

I have a version of this “equiripple 1D filter design” function in MATLAB, and I included it below. I made it significantly fancier than the research paper suggested, but nothing really fixed what it did wrong. I did get better results by using non-boxcar filters in frequency with a linear transition from stopband to passband, so that’s worth a try, though you might as well use Parks-McClellan still.

function [filter_coefficients, within_constraint, loops] = equiripple_1D( filter_order, freq_constraint, amp_constraint, mse_max, type_number )
%% equiripple_1D - FIR filter design using equiripple FFT algorithm. 
%   equiripple_1D( filter_order, filter_constraints ) creates an 
%   equiripple filter using the given
%   filter_constraints, and filter order. 
%   Inputs:
%       filter_order    - number of coefficients of designed filter. Will 
%                         be forced into an odd number if even number is 
%                         given.
%       freq_constraint - a n x 1 vector of numbers from 0 to 1 in
%                         normalized angular/radian frequency that
%                         determine with the amplitude constraint the ideal
%                         filter, and whether or not the filter comes
%                         within the constraints wanted. Basically, this
%                         determines the ripple allowed; put the maximum
%                         ripple you want for stop bands and 1-ripple for
%                         pass bands.
%       amp_constraint  - a n x 1 vector corresponding to freq constraints
%                         that gives amplitude minimums (in pass band) and 
%                         maximums (in stop band). Values should be between
%                         0 and 1 (as opposed to 0 to pi). 
%       mse_max         - maximum value of mean square error acceptable
%                         when designing filter. If left empty, defaults 
%                         to 1/10^order of your filter. 
%       type_number     - type of window you want to design the filter with
%                         in the iterative process. Expecting a number
%                         between 1 and 5. Defaults to 0. 
%                         0 - hamming window
%                         1 - rectangular window
%                         2 - triangular window
%                         3 - blackman window
%                         4 - gaussian window
%   Outputs:
%       filter_coefficients - coefficients of the FIR filter that the
%                             algorithm designed. Should be symmetrical and
%                             linear phase. 
%       within_constraint   - checks if filter is within constraints set
%                             initially and if not, returns a 0. Otherwise,
%                             returns a 1 if successful. Used if iterative
%                             designs with different parameters are
%                             required.

%% input checking

% make sure these are Nx1
freq_constraint = freq_constraint(:);
amp_constraint = amp_constraint(:);

% freq and amp constraints are the same size
assert( size( freq_constraint, 1 ) == size( amp_constraint, 1 ) );

% freq constraint is more than 0 or less than 1
assert( all( freq_constraint >= 0 ) && all( freq_constraint <= 1 ) );

% freq constraint also should be in ascending order
freq_constraint = sort( freq_constraint );

% amp constraint is more than 0 or less than 1 
%assert( all( amp_constraint >= 0 ) && all( amp_constraint <= 1 ) );

% make sure filter order is >0, and odd for now
if isempty( filter_order ) || filter_order < 3
    filter_order = find_ideal_order( freq_constraint, amp_constraint );
end
if rem( round(filter_order), 2 ) ~= 1
    filter_order = round(filter_order) + 1;
end

% make sure MSE maximum is actually set to something
if ~exist( 'mse_max', 'var' ) || isempty( mse_max ) || mse_max < 0 || mse_max > .5
    mse_max = 10^-filter_order;
end

% maks sure window is set
if ~exist( 'type_number', 'var' ) || type_number > 4 || type_number < 0 
    type_number = 0; 
end

%% actual design process

% create the ideal filter using constraints
ideal_filter = create_ideal_filter( filter_order, ...
                                    freq_constraint, ...
                                    amp_constraint );
                                
% iterative part, set up initial large error and previous filter 
mean_square_error = 9999;
ideal_filter_coefs = real( ifft( ideal_filter ) );
greater_part = (filter_order+1 )/2;
lesser_part = (filter_order-1)/2;
ideal_filter_coefs( (greater_part + 1):(end - lesser_part)  ) = 0;
work_filter = real( fft( ideal_filter_coefs ) );
previous_filter = zeros( filter_order, 1 );
loops = 0;
window_coef = make_window( filter_order, type_number );
window_coef = [ window_coef(greater_part:end) ; ...
                zeros( numel( ideal_filter_coefs ) - numel(window_coef), 1) ; ...
                window_coef(1:lesser_part) ];
    
while mean_square_error > mse_max
    loops = loops + 1;
    % shaping in frequency domain
    current_design = force_fft_shape( work_filter, ...
                                      ideal_filter, ...
                                      freq_constraint, ...
                                      amp_constraint );

    % zero out coefficients outside of our desired filter order
    %nz_current = current_design;
	current_design( (greater_part + 1):(end - lesser_part)  ) = 0;
    %current_design = current_design .* window_coef;
    for_error_checking = [current_design(1:greater_part) ; current_design(end-lesser_part+1:end) ];                              
    % check for mean square error, and then save current design as previous
    mean_square_error = find_mse( previous_filter, for_error_checking );
	previous_filter = for_error_checking;
	%mean_square_error = find_mse( nz_current, current_design );
    work_filter = real( fft( current_design ) );
    if loops > 1e6
        break;
    end
end

%check if within constraints, may be implemented later
if loops > 1000
    within_constraint = 0;
else
    within_constraint = 1;
end
current_design = current_design .* window_coef;
filter_coefficients = [current_design(1:greater_part) ; current_design(end-lesser_part+1:end) ];
end

%% subfunction for creating ideal filter
function coefficients = create_ideal_filter( filter_order, freq_constraint, amp_constraint )

% make constraints have 0 and 1 frequency, and idealized amplitudes
[freq_constraint, amp_constraint] = fix_constraints( freq_constraint, ...
                                                     amp_constraint );
% for ideal filter, turn amplitudes into 0s and 1s
amp_constraint = round(amp_constraint);

% find order of filter that can give us exact values we want.
% Inverse of greatest common divisor of all the freq_constraints
% will give us enough coefficients to hit exact freq_constraint
% locations
% design_order = 1;
% while (design_order <= filter_order) || any( rem( freq_constraint, 1/design_order ) > 0 ) 
%     design_order = design_order * 10;
% end
% design_order = design_order+1;
design_order = ( ( filter_order - 1 )/2 ) * 10 + 1;
% make ideal filter
coordinates = round( design_order .* freq_constraint );
coordinates(1) = 1;
coefficients = round( interp1( coordinates, amp_constraint, (1:design_order)') );
coefficients = [ coefficients; coefficients(end:-1:2) ];
end

%% subfunction for forcing FFT into constraints
function new_coefficients = force_fft_shape( work_filter, ...
                                             ideal_filter, ...
                                             freq_constraint, ...
                                             amp_constraint )
% get freq constraint with 0 and 1 appended
[freq_constraint, amp_constraint] = fix_constraints( freq_constraint, amp_constraint );
% for ideal filter, turn amplitudes into 0s and 1s
ideal_amp_constraint = round(amp_constraint);
% get coordinates to work with
coordinates = round( ( ( numel( ideal_filter )+1 )/2 ) .* freq_constraint );
coordinates(1) = 1;
% get a negative -1 where in stopband, 1 in passband
% pos_or_neg_ripple = 2*ideal_amp_constraint - 1;
min_ripple = min( abs( ideal_amp_constraint - amp_constraint ) );

%find where amp constraint remains in stop or remains in pass
no_change = find( diff( ideal_amp_constraint ) == 0 );
for index = no_change(:)'
    workpiece = work_filter( coordinates(index):coordinates(index+1) );
    work_ideal = ideal_filter( coordinates(index):coordinates(index+1) );
    try
        workpiece( workpiece > (work_ideal + min_ripple) ) = work_ideal(workpiece > (work_ideal + min_ripple)) + min_ripple;
    catch
    end
    try
        workpiece( workpiece < (work_ideal - min_ripple) ) = work_ideal(workpiece < (work_ideal - min_ripple)) - min_ripple;
    catch
    end
    work_filter( coordinates(index):coordinates(index+1) ) = workpiece;
end
% %need to force out all other ripples, using largest ripple factor found
% min_ripple = min( abs( ideal_amp_constraint - amp_constraint ) );
% top_bound = ideal_filter + min_ripple;
% low_bound = ideal_filter - min_ripple; 
% work_filter( work_filter > (ideal_filter + min_ripple) ) = top_bound( work_filter > (ideal_filter + min_ripple) );
% work_filter( work_filter < (ideal_filter - min_ripple) ) = low_bound( work_filter < (ideal_filter - min_ripple) );
% now constraints only worked on the first half, need to take it and
% flip it
greater_part = (numel(work_filter)+1)/2;
work_filter = [ work_filter(1:greater_part); work_filter(greater_part:-1:2) ];
new_coefficients = real( ifft( work_filter ) );
end
    
%% subfunction for error checking
function error = find_mse( previous_filter, current_design )
inside_part = (previous_filter - current_design).^2;
error = mean( inside_part );
end

%% subfunction for making constraints have ends
function [freq_constraint, amp_constraint] = fix_constraints( freq_constraint, amp_constraint )
% check if freq 0 and freq 1 are specified, and if not, stick them
% on the ends and copy amp constraints from closest point
if freq_constraint(1) ~= 0
    freq_constraint = [0; freq_constraint];
    amp_constraint = [amp_constraint(1); amp_constraint];
end
if freq_constraint(end) ~= 1
    freq_constraint = [freq_constraint; 1];
    amp_constraint = [amp_constraint; amp_constraint(end)];
end

end

function coefficients = make_window( filter_order, type_number )
% make a vector from 1 to filter_order, and find hamming window as long as
% the filter created.
n = 1:filter_order;
n = n - 1;
switch type_number
    case 0
        coefficients = .54 - .46 * cos( 2*pi*n./(filter_order - 1) );
    case 1
        coefficients = ones(filter_order, 1);
    case 2
        half_of_triangle = linspace( 0, 1, (filter_order-1)/2 )';
        coefficients = [half_of_triangle(1:end); half_of_triangle(end:-1:2)];
    case 3
        
    case 4
        
end
coefficients = coefficients(:);
end

function filter_order = find_ideal_order( freq_constraint, amp_constraint )
%find smallest ripple constraint
ideal_amp_constraint = round( amp_constraint );
min_ripple = min( abs( ideal_amp_constraint - amp_constraint ) );

%find smallest passband constraint
differences = diff(ideal_amp_constraint);
transition = find( differences ~= 0 );
transition_bw = min( freq_constraint( transition + 1 ) - freq_constraint( transition ) );

%calculate N; doing top part of fraction, bottom part, then ceiling because
%we need an integer N.
N = -20 * log10( min_ripple ) - 13;
N = N / (14.6*( transition_bw ) / (2*pi) );
filter_order = ceil( N );
end